Neural Theorem Provers

07 Oct 2019 Logic Learning Query answering Neural-Symbolic

This paper (Rocktäschel & Riedel, 2017) presents Neural Theorem Provers (NTP), a framework for fuzzy/real logic i.e. [0,1]-query answering with backwards chaining and subsymbolic representation learning.

Idea

We start with a first order logic language with no existential quantifiers or function symbols. Knowledge bases are composed of facts and rules in Horn clause format (ala Prolog).

We assign to each constant c and predicate P symbol a fixed length k vector \(\Theta\) i.e. \(\Theta_c \in \mathbb{R}^k\) and \(\Theta_P \in \mathbb{R}^k\).

Then, allow unification to match any two symbols (constant or predicate) and in turn add a loss to the query answer with respect to the difference between those two symbols.

Unification tree for a query:

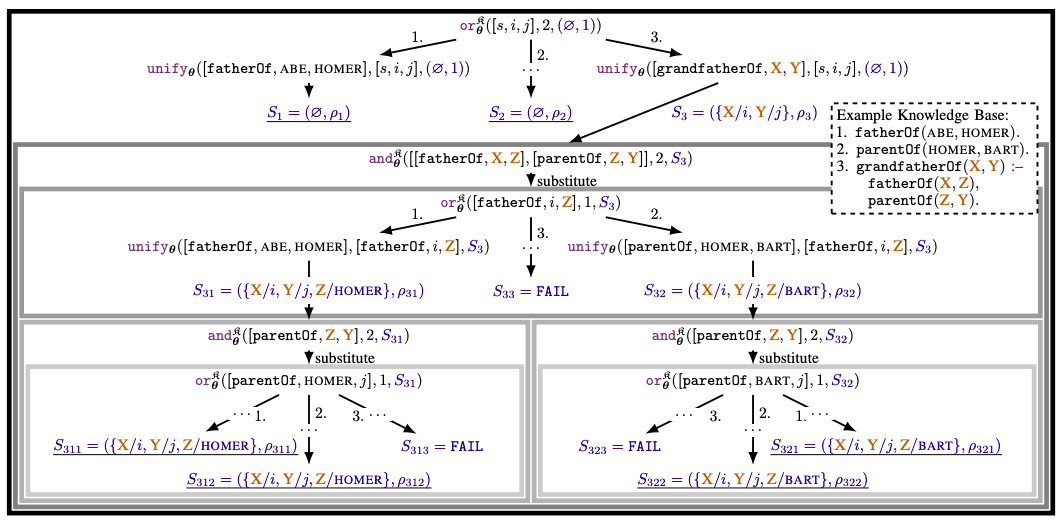
This is how symbols are unified:

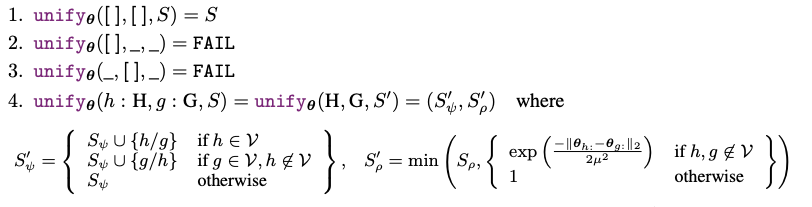
Example of unification:

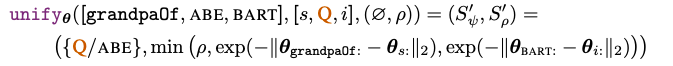
OR operation:

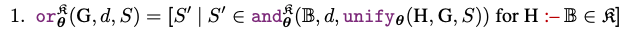
OR example:

AND operation:

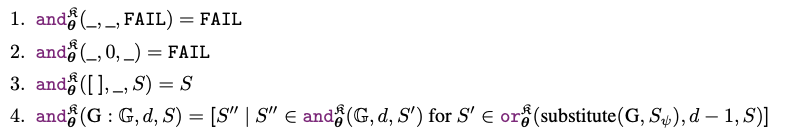
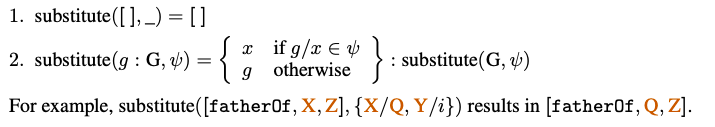
Finally, optimize vectors with respect to the well known facts of the knowledge base.

How

1. Start with a first order knowledge base which contains facts and rules (ala Prolog). No \(\exists\)-quantifiers and all variables are \(\forall\)-quantified implicitly.
2. Each symbol is assigned a random vector.
3. Take the known facts as positive examples and replace symbols with other (incorrect) ones to generate negative examples.
4. In each optimization/training pass run backwards chaining with a set of positive and negative examples as the goals (removing them from the knowledge base temporarily).
5. At each execution step a confidence score for one goal is calculated (even though we know if that goal is true or not), then we calculate the error of the whole training pass through the log-likelihood function and the gradient of the error with respect to the vector representation of each symbol.
6. After training pass, we slightly modify the vector representations according to their gradient to minimize the error. Repeat this \(n \in \textrm{N}\) times.

Results

• Achieved state-of-the-art accuracy with respect to ComplEx. Example dataset \(\textit{Nations}\) contains 56 binary predicates, 111 unary predicates, 14 constants and 2565 true facts. This method has a horrible time complexity because backwards chaining by itself is very demanding and doing it successively with large sets of examples leads to hard explosions. Note: proof depth is limited and no circular reasoning.
• Can learn vector representations that:
  1. Match symbols with identical meaning (\(\textit{ABC}\) and \(\textit{aBc}\)),
  2. Express similarity between related symbols (\(\textit{fatherOf}\) and \(\textit{parentOf}\)), and
  3. Enable to discover and utilize rules by using \(\textit{parametrized rules}\) in which the symbols are unknown but are assigned meaning through training (e.g. parametrized transitivity as \(p(X,Y) \text{ :- } q(X,Z), q(Z,Y).\)).

References

1. Rocktäschel, T., & Riedel, S. (2017). End-to-end differentiable proving. Advances in Neural Information Processing Systems, 3788–3800.