Logic Tensor Networks

08 Oct 2019 Logic Learning Query answering Neural-Symbolic

Logic Tensor Networks (Serafini & Garcez, 2016) is a framework for learning and reasoning combining neural-network capabilities with knowledge base data representation structures using first-order logic.

They address the problem of (i) query answering in the unit interval [0,1] (also known as fuzzy or real logic), as well as, (ii) subsymbolic (vector) representation finding of constant symbols, function symbols and predicates.

Idea

The framework takes as input a first-order logic knowledge base containing sentences and a target truth interval \([v,w] \subseteq [0,1]\) for each of them. Constant symbols (representing objects) are translated to (real space, fixed size) vectors, function symbols are intepreted as linear transformations and predicate symbols as non-linear mappings from real space vectors to the unit interval. These 3 types of mappings are performed via learnable parameters. A loss function models how far this mappings differ from the target truth intervals \([v,w]\). Then, these mappings are optimized resulting in constant, function and predicate symbol mappings that best replicate the truth interval modeled by the knowledge base.

How

The paper’s builds upon a (first-order) language \(\mathcal{L}\) with constant \(\mathcal{C}\), function \(\mathcal{F}\) and predicate \(\mathcal{P}\) symbols. Knowledge is represented through sentences (formulas) in skolemized conjuctive normal form e.g.: \(P(apple)\), \(\forall x P(apple) \rightarrow Q(apple, x)\), \(\forall x \forall y (Q(x,y) \rightarrow R(x,f(y)))\). Constants, functions and predicates are interpreted through a grounding \(\mathcal{G}\):

1. \(\mathcal{G}(c) \in \mathbb{R}^n \ \forall c \in \mathcal{C}\).

2. \(\mathcal{G}(f) \in \mathbb{R}^{n * arity(f)} \rightarrow\mathbb{R}^n \ \forall f \in \mathcal{F}\) s.t. \(\mathcal{G}(f(t_1,...,t_m)) = \mathcal{G}(f)(\mathcal{G}(t_1),...,\mathcal{G}(t_m))\).

3. \(\mathcal{G}(P) \in \mathbb{R}^{n * arity(P)} \rightarrow [0,1] \ \forall P \in \mathcal{P}\) s.t. \(\mathcal{G}(P(t_1,...,t_m)) = \mathcal{G}(P)(\mathcal{G}(t_1),...,\mathcal{G}(t_m))\), \(\mathcal{G}(\neg P(X)) = 1- \mathcal{G}(P(X)) \text{ and } \mathcal{G}(\phi_1 \lor \phi_2) = \mu (\mathcal{G}(\phi_1), \mathcal{G}(\phi_2))\).

where \(\mu\) is a t-conorm such as \(\mu(a,b) = min(a+b, 1)\).

More concretely,

• Constants \(\mathcal{G}(c_i) = \textbf{v}_i\) can be given or learned (and initialized randomly).

• Functions are learnable linear transformations:

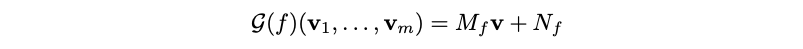
• Predicates are learnable non-linear transformations mapping to the unit interval given by:

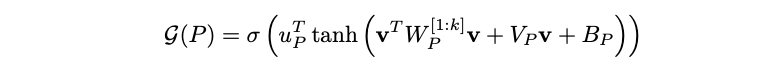
The knowledge is represented by what is called a grounded theory:

Then, the loss of a specific grounding which expands the initial partial grounding of a grounded theory is defined as:

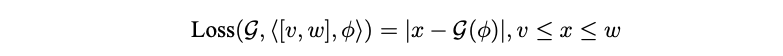
And finally, in order to restrict the grounding search space to a subset of grounding functions \(\mathbb{G}\) and a subset of clause instantiations \(K_0\):

In this case, \(\mathbb{G}\) is the space of groundings defined by (2) and (3) above, while clause instantiations \(K_0\) are every possible instance up until certain fixed depth k.

The problem of query answering is thus solved by our interpretations of the symbols in our logic vocabulary. Namely, given a query \(Q(c)\), recall that the grounding \(\mathcal{G}(Q(c)) \in [0,1]\) because \(\mathcal{G}(Q(c)) = \mathcal{G}(Q)(\mathcal{G}(c))\) where \(\mathcal{G}(c) \in \mathbb{R}^n\) and \(\mathcal{G}(Q) \in \mathbb{R}^n \mapsto [0,1]\).

To train, all clauses are grounded until depth k, the error is calculated as explained above, and groundings for constants, functions and predicate symbols are optimized successively until the error is minimized (through standard deep learning frameworks).

Results

• There is a Tensorflow implementation called ltn available in Github.
• The first order logic language presented is highly expressive, being able to support function symbols and the negation operator (with the open world assumption).
• Query answering becomes highly efficient as predicate and function symbols are interpreted as functions.
• Training is not efficient, as it require grounding all clauses (even limiting it to certain depth becomes problematic if the knowledge base is sufficiently large).
• From (Bianchi & Hitzler, 2019):
  1. Time to learn the parameters is highly influenced by the arity of the predicates.
  2. Satisfiability is strongly related with performance of the model: the higher the satisfiability the lower the error.
  3. More complex inferences (multi-hop) are more difficult to capture in the model.

References

1. Serafini, L., & Garcez, A. d’A. (2016). Logic tensor networks: Deep learning and logical reasoning from data and knowledge. ArXiv Preprint ArXiv:1606.04422.
   
2. Bianchi, F., & Hitzler, P. (2019). On the Capabilities of Logic Tensor Networks for Deductive Reasoning. AAAI Spring Symposium: Combining Machine Learning with Knowledge Engineering.